Áreas
Procedimentos para o cálculo das medidas de uma superfície plana. Método para calcular a área do quadrado, do losango, do paralelogramo, do triângulo, do retângulo, do polígono e do círculo geométrico.
Geometria Plana (formulário)
Fórmula para o cálculo da área das figuras geométricas. Triângulo, trapézio, paralelogramo, retângulo, losango, quadrado, círculo e polígono regular.
Geometria Espacial
Geometria de posição
Definição da relação entre espaço e volume e o desenvolvimento lógico da linguagem geométrica.
Geometria espacial
Ramo da geometria que estuda a medida do espaço ocupado por um sólido. Cálculo dos volumes de um cubo, prisma, pirâmide, cone, cilindro, esfera e de um paralelepípedo.
Geometria espacial (formulário)
Estrutura das figuras da geometria espacial. Paralelepípedo, cubo, prisma, pirâmide, cilindro e cone. Funções Trigonométricas no Triângulo Retângulo.
Poliedros
Poliedros são figuras espaciais limitadas por quatro ou mais polígonos chamados faces. As interseções das faces formam as arestas e as interseções das arestas formam vértices. Exemplos: cubos, paralelepípedos, prisma e pirâmide.
Sólidos de revolução
Definição de figuras e corpos gerados pelo movimento. Exemplos encontrados no dia-a-dia, como o cilindro (lata de refrigerante, uma pilha, um cano de água).
-> Baixar Programa que cria imagens de figuras de Geometrias Planas e Espaciais.
Exercicios
1) Calcule a área de cada um dos triângulos a seguir:
Resolução:
-> Baixar Programa que cria imagens de figuras de Geometrias Planas e Espaciais.
Exercicios
1) Calcule a área de cada um dos triângulos a seguir:
Resolução:
Apótema de uma pirâmide regular e apótema de sua base
Altura de uma pirâmide é à distância do vértice da pirâmide ao plano da base. À altura de cada uma das faces laterais chama-se apótema da pirâmide. É evidente que, sendo a base um polígono regular, este também tem um apótema, a que se chama apótema da base.
Numa pirâmide podemos encontrar os seguintes elementos:
- Base (polígono);
- Faces (triângulos);
- Arestas da base (lados da base);
- Arestas laterais (lados das faces que não pertencem à base);
- Vértices da base (vértices do polígono da base);
- Vértice da pirâmide (ponto de encontro das arestas laterais).
Assim, teremos:
- Pirâmide triangular (três faces; base é um triângulo);
- Pirâmide quadrangular (quatro faces);
- Pirâmide pentagonal (cinco faces);
- Pirâmide hexagonal (seis faces);
Exercicios:
Questão 1:
Em uma pirâmide regular quandrangular, cada aresta lateral mede 10 cm e cada aresta da base mede 12 cm.
Calcule:
a) a medida m do apoótema da pirâmide;
b) a medida r do apótema da base da pirâmide;
c) a medida H da altura da pirâmide;
d) a área lateral AL da pirâmide;
e) a área B da base da pirâmide;
f) a área total At da pirâmide;
g) o volume V da pirâimide;
Resolução:
Questão 2:
Em uma pirâmide regular triangular, cada aresta mede 2√13 cm e cada aresta da base mede 6√3 cm.
Calcule:
a) a medida m do apoótema da pirâmide;
b) a medida r do apótema da base da pirâmide;
c) a medida H da altura da pirâmide;
d) a área lateral AL da pirâmide;
e) a área B da base da pirâmide;
f) a área total At da pirâmide;
g) o volume V da pirâimide;
Resolução:
Números Complexos
Definições
Planificações:
Exercicios:
Questão 1:
Em uma pirâmide regular quandrangular, cada aresta lateral mede 10 cm e cada aresta da base mede 12 cm.
Calcule:
a) a medida m do apoótema da pirâmide;
b) a medida r do apótema da base da pirâmide;
c) a medida H da altura da pirâmide;
d) a área lateral AL da pirâmide;
e) a área B da base da pirâmide;
f) a área total At da pirâmide;
g) o volume V da pirâimide;
Resolução:
Questão 2:
Em uma pirâmide regular triangular, cada aresta mede 2√13 cm e cada aresta da base mede 6√3 cm.
Calcule:
a) a medida m do apoótema da pirâmide;
b) a medida r do apótema da base da pirâmide;
c) a medida H da altura da pirâmide;
d) a área lateral AL da pirâmide;
e) a área B da base da pirâmide;
f) a área total At da pirâmide;
g) o volume V da pirâimide;
Resolução:
Números Complexos
Definições
Vimos na resolução de uma equação do 2º grau que se o discriminante é negativo, ela não admite raízes reais. Por exemplo, a equação
x2 + 9 = 0
não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos:
x2 = -9
x = ±
mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada
Os números Complexos constituem o maior conjunto numérico existente.
N: conjunto dos números Naturais
Z: conjunto dos números Inteiros
Q: conjunto dos números Racionais
I: conjunto dos números Irracionais
R: conjunto dos números Reais
C: conjunto dos números Complexos
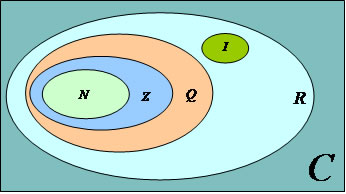
Os números Complexos constituem o maior conjunto numérico existente.
N: conjunto dos números Naturais
Z: conjunto dos números Inteiros
Q: conjunto dos números Racionais
I: conjunto dos números Irracionais
R: conjunto dos números Reais
C: conjunto dos números Complexos

.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2º grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.
Primeiro, eles definiram um novo número
i = 
Isso conduz a i2 = -1. Um número complexo é então um número da forma a + bi onde a e b são números reais.
Para a equação acima fazemos:
x = ± 
x = ± 
x = ±  .
. 
x = ± 3 i
As raízes da equação x2 + 9 = 0 são 3i e - 3i.
| Definição Um número complexo é uma expressão da forma a + bi onde a e b são números reais e i2 = -1.No número complexo a + bi, a é a parte real e b é a parte imaginária. Aritmética dos números complexos Adição e Subtração
|












 = 6 – 8i + 9i – 12
= 6 – 8i + 9i – 12 = – 8 – 4i + 4i + 2
= – 8 – 4i + 4i + 2