Um paralelepípedo retângulo com todas as arestas congruentes ( a = a = a ) recebe o nome de cubo. Dessa forma, as seis faces são quadrados.

Um cubo é o hexaedro regular. É um dos cinco Sólidos Platónicos.
db = diagonal da base

Um cubo é o hexaedro regular. É um dos cinco Sólidos Platónicos.
Tem 6 faces, 12 arestas e 8 vértices.
Planificação do Cubo
O Cubo tem 11 planificações ao todo. E são elas:
dc=diagonal do cubo
Na base ABCD, temos:
No triângulo ACE, temos:
Área e Volume
A área total A e volume V de um cubo de comprimento de aresta a são:
A = 6a2
V = a3
Esfera
História
O estudo da esfera remonta a uma época muito antiga. Segundo historiadores, o matemático grego Arquimedes de Siracusa (287-212 a.C.) aparece como o primeiro a escrever um tratado sobre a esfera e o cilindro, no qual ele estabelece relações entre as áreas e os volumes dos dois sólidos.
Conceito
A esfera no espaço R³ é uma superfície muito importante em função de suas aplicações a problemas da vida. Do ponto de vista matemático, a esfera no espaço R³ é confundida com o sólido geométrico (disco esférico) envolvido pela mesma, razão pela quais muitas pessoas calculam o volume da esfera. Na maioria dos livros elementares sobre Geometria, a esfera é tratada como se fosse um sólido, herança da Geometria Euclidiana.
Download do Programa
Posição relativa entre plano e esfera
Plano secante à esfera
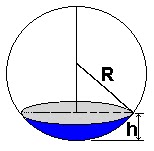
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.
O plano e a esfera não possuem pontos em comum.
Área de uma Superfície Esférica
Temos que a área de uma superfície esférica de raio r é igual a:

Volume da esfera
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:
Exemplos:
1) Um plano secciona uma esfera a 4 cm do centro 0, determinando uma secção plana de raio 3 cm. Calcule o volume dessa esfera e a área de superfície.
Resolução:
2) Duas esferas tangentes exteriormente e tangentes um plano nos pontos A e B tem raios iguais a 4 cm . Calcular a distância entre A e B.
Resolução:
Fuso Esférico e Cunha Esférica
Plano secante à esfera
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.
O plano e a esfera não possuem pontos em comum.
Temos que a área de uma superfície esférica de raio r é igual a:

Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:
Exemplos:
Resolução:
Resolução:
Fuso Esférico e Cunha Esférica
Azul: é o fuso
Cinza: é a cunha.
Fuso é uma parte da esfera, podendo ser representada por "goma de mexerica" (metaforicamente).
Exemplos:
1) Calcular o volume de uma cunha esférica de raio 3 cm cujo ângulo diedro mede 45°.
Resolução:
Video
Em Matemática, um cilindro é o objeto tridimensional gerado pela superfície de revolução de um retângulo em torno de um de seus lados. De maneira mais prática, o cilindro é um corpo alongado e de aspecto roliço, com o mesmo diâmetro ao longo de todo o comprimento.
- Base: É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.
- Eixo: É o segmento de reta que liga os centros das bases do "cilindro".
- Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
- Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
- Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
- Área lateral: É a medida da superfície lateral do cilindro.
- Área total: É a medida da superfície total do cilindro.
- Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
Área da base (Ab)
É a superfície de um círculo com o raio R.
Volume do Cilindro (V)
O volume do cilindro é igual ao volume de um prisma, ou seja, possui a mesma altura e base.
Principais Fórmulas de um Cilindro
Para se determinar a medida da área lateral do tronco do cilindro é necessário realizar a operação entre o produto do comprimento da circunferência e o segmento do eixo.

Para se determinar o volume do tronco do cilindro é necessário realizar a operação entre o produto da área de secção e o segmento do eixo.

2) Um cilindro circular reto de altura 5 m, o raio da base mede 2 m. Calcule, desse cilindro:
a) a área lateral AL;
b) a área B de uma base;
c) a área total AT;
d) o volume V;
Resolução:
Video
Cone
- Vértice de um cone é o ponto P, onde concorrem todos os segmentos de reta.
- Base de um cone é a região plana contida no interior da curva, inclusive a própria curva.
- Eixo do cone é quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.
- Geratriz é qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.
- Altura é a distância do vértice do cone ao plano da base.
- Superfície lateral de um cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.
Exemplos:
1) Calcular o volume de uma cunha esférica de raio 3 cm cujo ângulo diedro mede 45°.
Resolução:
Video
Cilindro
Em Matemática, um cilindro é o objeto tridimensional gerado pela superfície de revolução de um retângulo em torno de um de seus lados. De maneira mais prática, o cilindro é um corpo alongado e de aspecto roliço, com o mesmo diâmetro ao longo de todo o comprimento.
Objetos geométricos em um "cilindro"
Em um cilindro, podemos identificar vários elementos:
- Eixo: É o segmento de reta que liga os centros das bases do "cilindro".
- Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
- Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
- Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
- Área lateral: É a medida da superfície lateral do cilindro.
- Área total: É a medida da superfície total do cilindro.
- Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
É a superfície de um círculo com o raio R.
Volume do Cilindro (V)
O volume do cilindro é igual ao volume de um prisma, ou seja, possui a mesma altura e base.
Principais Fórmulas de um Cilindro
Tronco do Cilindro

Para se determinar o volume do tronco do cilindro é necessário realizar a operação entre o produto da área de secção e o segmento do eixo.

Exemplos:
1) Em um cilindro circular reto de altura 8 cm, o raio da base mede 3 cm. Calcular desse cilindro.
a) a área lateral;
b) a área da base;
c) a área total;
d) a área da secção merediana;
e) o volume.
Resolução:
2) Um cilindro circular reto de altura 5 m, o raio da base mede 2 m. Calcule, desse cilindro:
a) a área lateral AL;
b) a área B de uma base;
c) a área total AT;
d) o volume V;
Resolução:
Video
Cone
Um cone é um sólido geométrico formado por todos os segmentos de reta que têm uma extremidade em um ponto V (vértice) em comum e a outra extremidade em um ponto qualquer de uma mesma região plana R (delimitada por uma curva suave, a base).
Os cones podem ser divididos em:
1- Reto
2- Oblíquo
3- Equilátero
Reto
O cone é dito reto quando a sua base é uma circunferência e a reta que liga o vértice superior ao centro da circunferência da sua base é perpendicular ao plano da base. Em um cone circular reto, cuja base é um círculo, a face lateral é formada por geratrizes (g), que são linhas retas que ligam o vértice superior a pontos constituintes da circunferência do círculo.
Reto
Oblíquo
Denomina-se oblíquo quando não é um cone reto, ou seja, quando o eixo é oblíquo ao plano da base.
Equilátero
Um cone circular reto é um cone equilátero se a sua seção meridiana é uma região triangular equilátera e neste caso a medida da geratriz é igual à medida do diâmetro da base.
- Base de um cone é a região plana contida no interior da curva, inclusive a própria curva.
- Eixo do cone é quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.
- Geratriz é qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.
- Altura é a distância do vértice do cone ao plano da base.
- Superfície lateral de um cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.
- Superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.
- Seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.
Fórmulas
V = (Ab.h) / 3
Exemplos:
1) Em um cone circular reto de altura 12 cm, o raio da base mede 5 cm. Calcular desse cone:
a) a área lateral
b) a área da base
c) a área total
d) o volume
e) a medida O do ângulo central equivalente à superficie lateral do cone.
f) a área da secção meridiana.
Resolução:
Fórmulas
Área da Base
Ab =π.r²
Área de um setor circular
A = (l. r) /2
Área lateral
Al = π.r.g
Área Total
At =Ab+ Al
Volume
Exemplos:
1) Em um cone circular reto de altura 12 cm, o raio da base mede 5 cm. Calcular desse cone:
a) a área lateral
b) a área da base
c) a área total
d) o volume
e) a medida O do ângulo central equivalente à superficie lateral do cone.
f) a área da secção meridiana.
Resolução:
2) Em um cone circular reto de altura 6 cm, o raio da base mede 8 cm. Calcule, desse cone:
a) a área lateral;
b) a área da base;
c) a área total;
d) a medida O do ângulo central equivalente à superficie lateral do cone;
e) a área da secção meridiana;
f) o volume.
Resolução:
3) Em um cone circular de 4 m de altura, o raio da base mede 2 m. Um plano, paralelo à base desse cone e distante 2 de seu vértice, separa - o em dois sólidos.
Resolução:
Video